WT*

Upper convex hull

Given is an array of n points, the task is to compute the upper part of the convex hull. In particular, the output should be an array of points, containing the upper-hull points from left to right.

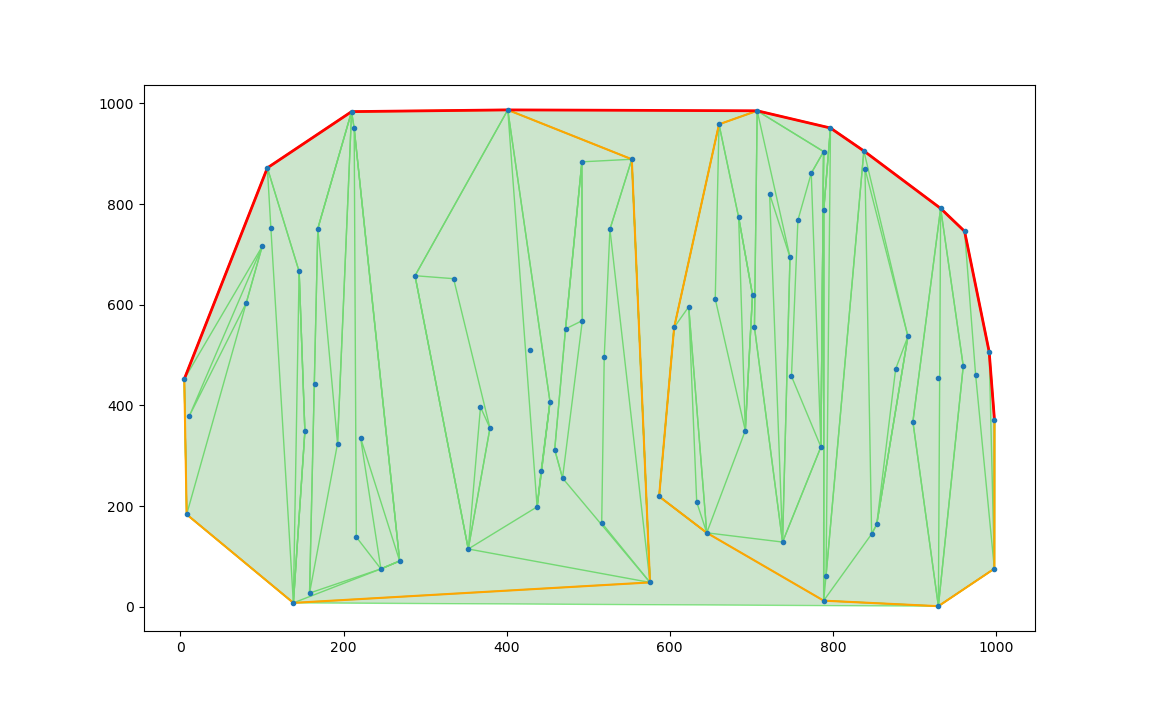
We present a divide-and-conquer techinque. We first sort the points according to the x coordinate. The procedure works on sub-arrays defined by an interval l-r, and returns the number of points in the hull. The actual points are copied to occupy consecutive places in A starting from l (thus the procedure is destructive to A). First, the interval is divided into two halves, and the upper hulls are computed. The hull points are then copied to temporary arrays HL and HR.

Next, we need to find a common tangent: one point on each of the hulls such that all other points are below the line defined by them. Since the hulls are convex, it is easy to find a tangent from a point on a left hull to the right hull:

int tangent_point(point from, point P[_]) {
  int result = 0;
  int n = P.size;
  if (n < 2) return n - 1;
  pardo(i : P.size) if (test_hit_lr(from, i, P) == 0) result = i;
  return result;
}

where the test_hit_lr function tests, whether the line from-P[i] is tangent to the hull P[0]...P[P.size-1] assuming from is to the left of P. It returns 0 if it is a tangent, -1 or 1 if the tangent point is to the right or left on P. The test itself just checks the orientation (dir_cw,dir_ccw) of the neighboring points:

int test_hit_lr(point from, int i, point P[_]) {
  if (i < 0) return -1;
  if (i >= P.size) return 1;
  if (P.size == 1) return 0;
  if (i == 0) {
    if (dir_cw(A[from], P[i], P[i + 1])) return 0;
    return -1;
  }
  if (i == P.size - 1) {
    if (!dir_ccw(from, P[i], P[i - 1])) return 0;
    return 1;
  }
  if (dir_ccw(from, P[i], P[i - 1])) return 1;
  if (!dir_cw(from, P[i], P[i + 1])) return -1;
  return 0;
}

Finally, the common tangent can be found by trying, in parallel, all points on the left hull.

However, finding the common tangent by brute force results in quadratic work in the worst case. We can use p-ary search to fix it. Replace the tangent-finding code by the following:

// if HL is small, find the tangent by brute force
    if (s[0]<9){
      pardo(i : s[0]) {
        // find a tangent from HL[i] to HR
        int t = tangent_point_p_ary(0,HR.size-1,HL[i],HR,sqrt(HR.size));
        // if it also a tangent from HR[t] to HL, we have the result
        if (test_hit_rl(HR[t],i,HL)==0) {
          tl=i;tr=t;
        }
      }
    }
    else {
      // partition into sqrt intervals
      int sn = sqrt(s[0])-1;
      int hits[sn];
      int result=-1;
      int li = (sn-1)*sn, ri=s[0]-1;
      pardo (i:sn-1) {
        // fint the tangents for boundaries of intervals
        int j = (i+1)*sn;
        int  t = tangent_point_p_ary(0,HR.size-1,HL[j],HR,sqrt(HR.size));
        int hit = test_hit_rl(HR[t],j,HL);
        hits[i]=hit;
        if (hit==0) {
          // direct hit, we have the result
          result=j; tl=j;tr=t;
        }
        if (hit==1) {
          // this point is to the right and the previous is to the left (or does not exist)
          // we have found the proper bucket
          if (i==0) {li=0;ri=sn;}
          else if (hits[i-1]==-1) {li=i*sn;ri=(i+1)*sn;}
        }
      }
      // if there wasn't a direct hit, 
      // check the found interval by brute force
      if (result==-1)
      pardo(i : ri-li+1) {
        int t = tangent_point_p_ary(0,HR.size-1,HL[li+i],HR,HR.size);
        if (test_hit_rl(HR[t],li+i,HL)==0) {tl=li+i;tr=t;}
      }
    }